之前讨论了整数量子霍尔效应

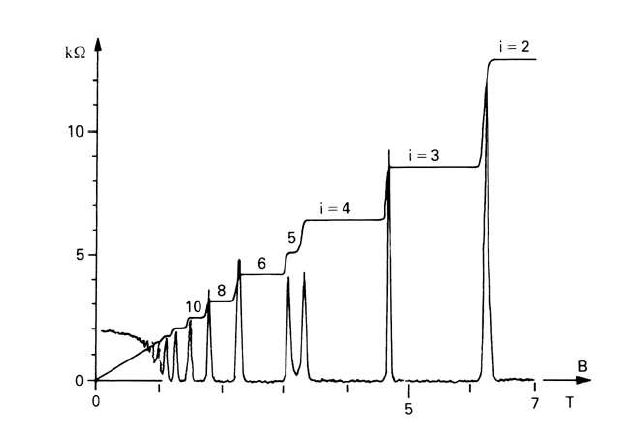
弱磁场的情况下，非对角的霍尔电导和磁场强度满足经典的线性关系，强磁场作用下出现了很多量子化Hall的平台，其 Hall conductance 正比 Berry curvature在Brillouin zone的积分，

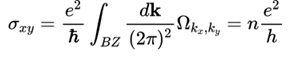
其中Berry curvature和Berry connection为

Hall conductance的量子化平台取决于这个积分

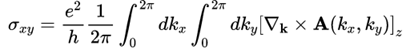
叉乘展开并作个分布积分可得

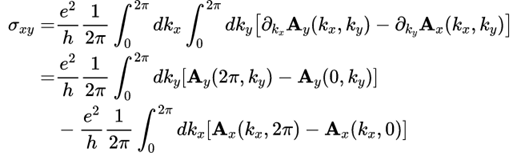
等价于看Berry connection在0和2π的变化的积分，由于周期性边界条件的限制，0和2π处的波函数只相差一个phase

有

类似的有

代入Hall conductance可得

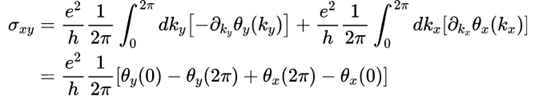
且有边界条件

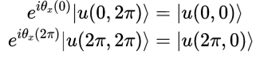
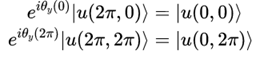
可得

即

从而证明了Berry curvature积分是2π的整数倍以及Hall conductance的量子化，也证明了拓扑不变量Chern number ( first Chern number也叫TKNN number) 必须是整数

1. SHUN-QING. SHEN. Topological Insulators: Dirac Equation in Condensed Matter. Springer, 2018.